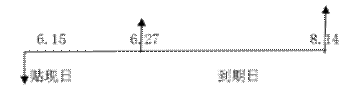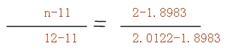|
|
||||||||||||||||||||||||
|
3.1.货币时间价值 1.货币时间价值的含义 货币的时间价值,又称资金时间价值,是指货币经历一定时间的投资和再投资所增加的价值。在商品经济中,存在这样一种现象:今天你将100元钱存入银行,假定利息率为5%,一年后的今天,你将会得到105元。其中的100元是本金,5元的利息就是这100元钱经过一年时间的投资所增加的价值,该利息就是货币时间价值。但并非所有货币都具有时间价值,货币具有时间价值的前提条件是货币只有当作资本投入生产和流通后才能产生增值。 2.货币时间价值的实质 根据马克思的劳动价值理论,在发达的商品经济条件下,资本流通的公式是:G-W-G,其中,G= G+△G,即原来预付的货币额G加上一个增值的货币额△G。处于两端的属于同一性质的货币,若两个货币量完全相等,投资行为就失去了实际意义。所以,资本流通的结果不仅要保持原有资本的价值,而且还要取得更多的价值即增值。由此可见,货币时间价值的真正来源是工人创造的剩余价值的一部分。 3.货币时间价值的表现形式 货币时间价值有两种表现形式:一种是相对数(时间价值率)。它是指在没有风险和没有通货膨胀条件下的社会平均资金利润率或平均报酬率。在实际工作中,人们习惯使用相对数表示货币的时间价值;另一种是绝对数(时间价值额)。它是指资金在生产经营过程中带来的增值额,它等于投资额与时间价值率的乘积。 4.货币时间价值的意义 货币的时间价值是客观存在的经济范畴。任何企业的财务活动都是在特定的时空中进行的。离开了时间价值因素,就无法正确计算不同时期的财务收支,也无法正确评价企业盈亏。因此,货币的时间价值是企业进行财务决策的基础。 (1)货币时间价值是企业筹资决策的重要依据。在筹资活动中,筹资时机的选择、举债期限的选择、资本成本的确定以及资本结构的决策等都要考虑时间价值因素。 (2)货币时间价值是企业投资决策的重要依据。在投资活动中,树立货币时间价值理念,能够从动态上比较投资项目的各种方案在不同时期的投资成本、投资报酬,提高投资决策的正确性;能够使投资者有意识地加强投资经营管理,降低投资成本,缩短投资项目建设期,提高投资效益。 (3)货币时间价值是企业经营决策的重要依据。在企业经营活动中,分期付款销售的定价决策,商品发运结算时间的决策,积压物资的降价处理决策以及流动资金周转速度的决策等都要考虑时间价值因素。 在考虑货币时间价值,分析资本运动和现金流量时应明确现值和终值两个基本概念。 1.现值 现值是指在未来某一时点上的一定数额的资金折合成现在的价值,在商业上俗称“本金”。通常记作P。 2.终值 终值是指现在一定数额的资金经过一段时期后的价值,在商业上俗称“本利和”。通常记作F。 终值与现值是一定数额的资金在前后两个时点上对应的价值,其差额就是货币时间价值。在现实生活中,计算利息时的本金、本利和相当于货币时间价值理论中的现值和终值。 为了计算方便,本章假定有关字母的含义:I—利息;F—终值,即本利和;P—现值,即本金;i—利率(或折现率);n—期数。 1.单利的计算 单利是指计算利息时只按本金计算利息,其所生利息不再加入本金重复计算利息,即本能生利,利不能生利。目前我国银行存贷款一般都采用单利计算利息。 (1)单利终值的计算。单利终值是指现在的一定量资金按单利计算的未来价值。其计算公式是:
F =P + I = P + P×i×n =
P(1+ i×n) (2)单利现值的计算。单利现值是指在未来某一时点上的一定量资金折合成现在的价值。其计算公式是:P = F/(1+ i×n) 而在票据贴现业务中,计算票据的贴现价值所采用的计算公式是:P = F-I ,其中,I是票据贴现利息。 实例3-1 商业汇票贴现业务 资料:BBC公司持有一张带息期票,面值为1200元,票面利率为4%,出票时间为 要求:(1)计算票据到期的利息。 (2)计算票据到期的终值 (3)因公司急需用款,于
图3-1 票据贴现业务的现金流量图 解答: (1)票据到期的利息I=P×i×n=1200×4%×(60/360)=8(元) (2)票据到期的终值F=P+I=1200+8=1208(元) (3)银行应付给企业P=F-I=F(1-i×n)=1208[1-6%×(48/360)]=1198.34(元) 注意:本公式中的I、i均为银行的贴现利息和贴现利率。 课堂讨论:试从财务角度分析票据贴现的实质 2.复利的计算 复利是指不仅本金计算利息,而且本期所生利息在下期并入本金一起计算利息,即本能生利,利也能生利,俗称“利滚利”。货币时间价值通常是按复利计算的。 (1)
复利终值的计算。复利终值是指现在的一定量资金按复利计算的未来价值。计算复利终值时,每期期末计算的利息应加入下期的本金形成新本金,再计算下期的利息,逐期滚算,其计算原理如表3-1所示。 表3-1 复利终值计算公式的推导过程
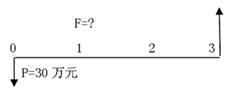
由表可得:n期复利终值的计算公式为:Fn =P(1+i)n 式中的(1+i)n为“1元的复利终值系数”,记为(F/P,i,n),可查“1元的复利终值系数表”求得,见附表一。 上式也可以写为:Fn =P(F/P,i,n) 即:复利终值=现值×复利终值系数 实例3-2 复利终值的计算 资料:BBC公司从银行取得贷款30万元,年利率为6%,贷款期限3年,第3年末一次偿还,贷款到期时公司应向银行偿还多少钱?
解答:已知P=30万元 i=6% n=3年 贷款到期时公司应向银行偿还的本利和为: F =P(1+i)n=P(F/P,i,n)=30×(F/P,6%,3)=30×1.191=35.73(万元) 图3-2 一次性收付款项终值的现金流量图 点评:查表方法——“1元的复利终值系数表”的第一行是利率i,第一列是计息期数n,相应的(F/P,i,n)在其纵横相交处。 (2)复利现值的计算 复利现值是指未来一定时间的特定资金按复利计算的现在价值。由n期复利终值计算公式Fn =P(1+i)n 可推到求得:Pn = Fn/(1+i)n = Fn
(1+i)-n 式中的(1+i)-n为“1元的复利现值系数”,记为(P/F,i,n),可查“1元的复利现值系数表”求得,见附表二。 上式也可以写为: Pn = F(P/F,i,n) 即:复利现值=终值×复利现值系数 实例3-3 复利现值的计算 资料:BBC公司欲投资A项目,预计5年后可获得600万元的收益,假定年利率(折现率)为10%。 要求:计算该笔收益的现值? 解答:
图3-3 一次性收付款项现值的现金流量图 P = Fn/(1+i)n
= Fn (1+i)-n= Fn(P/F,i,n) = 6000 000×(P/F,10%,5)= 6000 000×0.6209 = 3 725 400(元) (3)不等额系列收付款项的终值和现值的计算 在实际工作中,许多情况是发生系列不等额系列收付款项,因此经常需要计算不等额现金流量的终值之和或现值之和。 不等额系列收付款项终值的计算公式是: F = 不等额系列收付款项现值的计算公式是: P = 实例3-4 复利终值与现值的综合运用 资料:BBC公司2001年年初对A设备投资100
000元,该项目2003年年初完工投产;2003年至2005年各年末预期收益分别为20 000元、30 000元、50
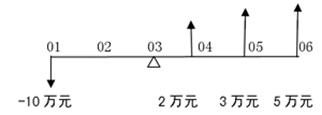
000元;银行存款复利利率为10% 要求:(1)计算2003年年初投资额的终值和2003年年初各年预期收益的现值之和。 (2)该投资项目是否可行 解答:该投资项目的现金流量如图:
图3-4 项目投资的现金流量图 (1)2003年年初投资额的终值F=P(1+i)n =P(F/P,i,n)=100 000×(F/P,10%,2)
=100 000×1.21 =121 000(元) (2)2003年年初各年预期收益的现值之和 ∑P=F04(P/F,i,n)+
F05(P/F,i,n)+F06(P/F,i,n)
=20 000×(P/F,10%,1)+30 000×(P/F,10%,2)+50 000×(P/F,10%,3)
=20 000×0.9091+30 000×0.8264+50 000×0.7513
=80 539(元) (3)该投资项目在2003年年初时,其收益小于支出,故该投资项目不可行。 点评:货币具有时间价值,不同时点上的收支不能直接比较,因而在筹资、投资分析中通常是以现值为基础进行各方案的比较,使发生在不同时点上的资金具有合理的、共同的可比基础。 实例3-5 内插法的运用 资料:BBC公司现有资本100万元,想投资报酬率为6%的投资机会,问经过多少年投资后才可能使现有资本增加1倍? 解答:已知P=100万元,F=2×100=200万元,i=6%, ∵ Fn =P(1+i)n
即 200=100(1+6%)n (1+6%)n=2 即(P/F,6%,n)=2 查表得: n=11
1.8983
n=?
2.00
n=12
2.0122 根据内插法原理:
解得:n=11.89(年) 因此,在11.89年以后可以使现有资本增加1倍。 点评:1. 内插法是财务管理学中运用较广的方法。 2.货币时间价值的计算中,已知三个变量(i或n,P,F),求n或i时,应先求出现值系数或终值系数,再应用内插法求出n或i. 3.年金的计算 年金是指一定时期内等额、定期的系列收付款项,通常记为A。如折旧、租金、养老金、等额分期付款、等额分期收款以及零存整取等都是年金问题。 年金的形式多种多样,根据其每次收付发生的时点不同,可分为普通年金、预付年金、递延年金、永续年金。见表3-2 表3-2
各种年金的特点与现金流量
(1)普通年金的计算 普通年金,又称后付年金,是指一定期限内每期期末等额收付的系列款项。
普通年金终值是指一定时期内每期期末等额收付的复利终值之和。其计算原理如表3-3所示。 表3-3
普通年金终值计算原理
由表3-3可知,普通年金终值的计算公式及其推导如下: FA= FA1+ FA2+ FA3+……+ FA(n-1)+ FA(n) =
A(1+i)n-1+ A(1+i)n-2 + A(1+i)n-3+……+ A(1+i)1+ A(1+i)0
① 将①式两端同时乘以(1+i),得: (1+i)FA=
A(1+i)n+ A(1+i)n-1 + A(1+i)n-2+……+ A(1+i)2+ A(1+i)1
②
用②式减去①式,得: i×FA=
A(1+i)n-A
= A×[(1+i)n-1]
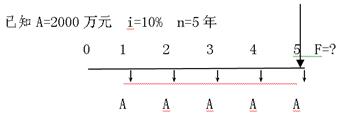
FA= A×{ [(1+i)n-1]}/ i 式中的[(1+i)n-1]/i称为“1元年金的终值系数”,记为:(F/A,i,n),可查“1元年金的终值系数表”求得,此表见附录三。 上式也可以写为:FA = A(F/A,i,n) 即:普通年金终值=年金×普通年金终值系数 实例3-6 普通年金终值的计算 资料:BBC公司计划在5年内每年年末向银行借款2000万元,借款年利率为10%,那么该公司在年末应付银行本息总额是多少? 解答:
图3-5 普通年金的现金流量图 FA = A(F/A,i,n)=2000×(F/A,10%,5)=2000×6.1051=122 10.2(万元) 实例3-7 年偿债基金的计算 资料:BBC公司有一笔5年后到期的借款,金额为10万元,公司为了能到期偿还该笔借款设立了偿债基金,年借款利率为8%。 要求:试计算从现在起每年年末需存入银行多少钱,才能到期偿清该笔借款? 解答:已知P=10万元 i=8% n=5年 由公式FA = A(F/A,i,n)得:
A= FA/(F/A,i,n)=100
000/(F/A,8%,5) =100 000/5.8666=17 045.65(元) 该公司从现在起每年年末需存入银行17 045.65(元),就能到期偿清该笔借款 点评:1. 偿债基金是指为了使年金终值达到既定金额,每年年末应收付的年金数额。在现实经济生活中,企业为了在约定的未来某一时点清偿某笔债务或积累一定数额的资金而必须分次等额提取的存款准备金,即偿债基金。
式中分式称作“偿债基金系数”,记作(A/F,i,n),等于普通年金终值系数的倒数。 普通年金现值是指一定时期内每期期末等额收付的复利现值之和。其计算原理如表3-4所示。 表3-4
普通年金现值计算原理
由表可知,普通年金现值的计算公式及其推导如下: PA= PA1+ PA2+ PA3+……+ PA(n-1)+ PA(n) =
A(1+i)-1+ A(1+i)-2 + A(1+i)-3+……+ A(1+i)-(n-1)+ A(1+i)-n
① 将①式两端同时乘以(1+i),得: (1+i)PA=
A(1+i)0+ A(1+i)-1 + A(1+i)-2+……+ A(1+i)-(n-2)+ A(1+i)-(n-1)
②
用②式减去①式,得: i×PA=
A-A(1+i)-n
= A[1-(1+i)-n]
所以:
PA= A[1-(1+i)-n]/i 式中的[1-(1+i)-n]/i称为“1元年金的现值系数”,记为:(P/A,i,n),可查“1元年金的现值系数表”求得,此表见附录四。 上式也可以写为:PA = A(P/A,i,n) 即:普通年金现值=年金×普通年金现值系数 实例3-8 年资本回收额的计算 资料:BBC公司想投资100万元购置一条生产线,预计可使用3年,社会平均利润率为8%。 要求:试计算该生产线每年至少给公司带来多少收益该投资才是可行的? 解答:已知P=100万元 i=8% n=3年
图3-6 一次性收付款项现值的现金流量图 由公式PA=
A[1-(1+i)-n]/i 可知: A =
PA/[1-(1+i)-n]/i= PA/(P/A,i,n) =100/(P/A,8%,3)=100/2.5771=38.8(万元) 点评:1. 年资本回收额是指为了使年金现值达到既定金额,每年年末应收付的年金数额。年资本回收额是年金现值的逆运算。其计算公式为:
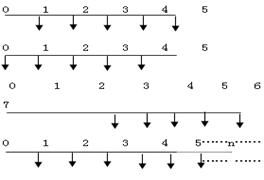
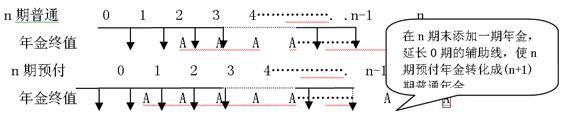
(2)预付年金的计算 预付年金,又称即付年金,是指一定期限内每期期初等额收付的系列款项。预付年金与普通年金的区别仅在于收付款时间的不同。 预付年金终值是指一定时期内每期期初等额收付款项的复利终值之和。 将普通年金视为标准年金,预付年金终值与普通年金终值之间的关系如图所示。
图3-7 预付年金终值计算原理图 由图可知:n期预付年金与n期普通年金的收付次数相同,收付发生的时间不同,利用图形变换将n期预付年金转化为(n+1)期普通年金,然后求n期预付年金的终值。 n期预付年金终值FA=FA(n+1)-A
=A(F/A,i,n+1)-A
=A[(F/A,i,n+1)-1] 即:预付年金终值=年金×预付年金终值系数 式中的[(F/A,i,n+1)-1]称为“预付年金终值系数”,可查“1元年金的终值系数表”的(n+1)期的值,然后减去1便可得到对应的n预付年金终值系数。 预付年金现值是指一定时期内每期期初等额收付款项的复利现值之和。 将普通年金视为标准年金,预付年金现值与普通年金现值之间的关系如图所示。
图3-8 预付年金终值计算原理图 由图可知:n期预付年金与n期普通年金的收付次数相同,收付发生的时间不同,利用图形变换将n期预付年金转化为(n-1)期普通年金,然后求n期预付年金现值。 n预付年金现值PA=PA(n-1)+A
=A(P/A,i,n-1)+A
=A[(P/A,i,n-1)+1] 即:预付年金现值=年金×预付年金现值系数 式中的[(P/A,i,n-1)+1]称为“预付年金终值系数”,可查“1元年金的现值系数表”的(n-1)期的值,然后加上1便可得到对应的n预付年金现值系数。 (3)递延年金的计算
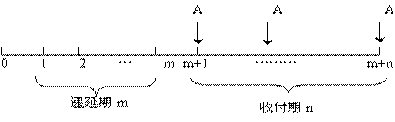
递延年金是指第一次收付发生在第二期或以后各期的年金。递延年金是普通年金的特殊形式。假设递延期为m,从第m+1期开始连续n期发生等额收付款项,递延年金的现金流量图如图所示。 递延年金终值与递延期数无关,其计算方法与普通年金终值相同。 递延年金现值的计算方法有三种: 第一种方法:假设递延期也有年金,先求出(m+n)期的年金现值,再减去递延期的年金现值。其计算公式是: 递延年金现值PA=A×(P/A,i,n+m)- A×(P/A,i,m) =A×[(P/A,i,n+m)- (P/A,i,m)] 第二种方法:分段计算递延年金的现值。先将递延年金视为普通年金,求出其递延期末的年金现值,再将此现值转换成第一期期初的现值。如图3-10所示:
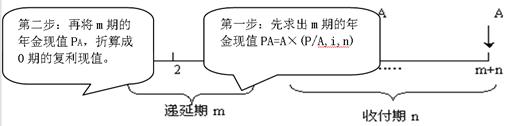
图3-10 递延年金的求现值原理图 其计算公式是:递延年金现值PA=A×(P/A,i,n)×(P/F,i,m) 第三种方法:分段计算递延年金现值。先将递延年金视为普通年金,求出其普通年金终值,再将此终值转算成第一期期初的现值。
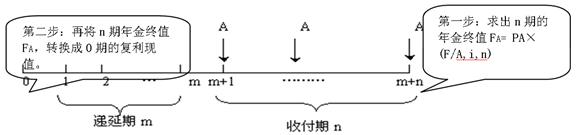
图3-11 递延年金的求现值原理图 其计算公式是:递延年金现值PA=A×(F/A,i,n)×(P/F,i,n+m) 实例3-9 递延年金终值与现值的综合应用 资料:BBC公司拟购置一处房产,房主提出两种付款方案:(1)从现在起,每年年初支付20万元,连续支付10次,共200万元;(2)从第5年开始,每年年初支付25万元,连续支付10次,共250万元。(1997年注册) 假设该公司的资金成本率(即最低报酬率)为10%,你认为该公司应选择哪个方案? 解答:(1)计算两个方案的现值 方案Ⅰ:预付年金的现值PA= A[(P/A,i,n-1)+1]=20[(P/A,i,n-1)+1]
=20[(P/A,10%,9)+1]=20[5.7590+1]=135.18(万元) 方案Ⅱ: 递延年金的现值PA=A×(P/A,i,n)×(P/F,i,m)
= 25×(P/A,10%,10)×(P/F,10%,3)
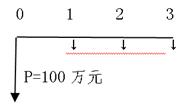
=25×6.1446×0.7513=115.41(万元) (2)因为方案Ⅰ的现值大于方案Ⅱ的现值,故该公司应选择方案Ⅱ. 点评: 计算递延年金的现值可采用三种不同的方法,但要注意年金发生的时点. (2)永续年金的计算 永续年金是指无限期支付的年金。在实际生活中,优先股股利、无限期债券、奖励基金等都属于永续年金。 由于永续年金期数无限,没有终止的时间,因此永续年金没有终值。 永续年金现值可以从普通年金现值的计算公式中推导出来:
实例3-10 永续年金的应用 资料: 某学校拟建立一项永久性的奖学金,每年计划颁发20 000元的奖学金,若银行存款利率为8%。 要求:试计算该学校现在应存入多少钱? 解答:P=A/i=20000÷8%=250000(元) |
||||||||||||||||||||||||
|
西藏民族学院 财经 学院 会计教研室制作 |